MATEMÁTICAS 6. ÁREA DEL CÍRCULO

¡Buenos días!

Hoy vamos a terminar con el tema de las áreas de las figuras planas, solo nos queda ver una: EL CÍRCULO.

En esta caso, ya no se trata de un polígono, porque sus lados no son líneas rectas.

Sus lados son una línea curva y cerrada cuyos puntos están todos a la misma distancia del centro.

¡Estoy segura de que os suena esta definición! 😎

Efectivamente: el contorno o el perímetro del círculo se llama circunferencia.

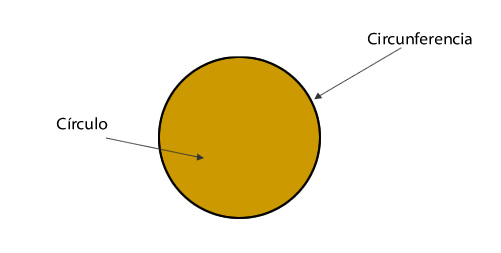
¿Recordáis que el curso pasado aprendimos a calcular la longitud de la circunferencia? 

¿Recordais que para ello nos hacía falta el número Π?

Seguro que recordáis también que el número Π (leído "pi") es igual a 3,1416 (redondeando, ya sabéis que es un número irracional con infinitas cifras decimales).

Pues esta era la fórmula para calcular la longitud de la circunferencia: 

                         L= 2.Π.r
          ____________________________________________________________________


Bueno, pues recordado todo esto vamos a pasar ya a ver cómo se calcula el área de cualquier círculo.

Os traigo a la misma profe de ayer, lo explica muy clarito y lo vais a entender muy bien si la escucháis con mucha atención. ¡Vamos allá!

VÍDEO

Bueno, pues ya sabemos que la fórmula para calcular el érea del círculo es: 

                                            

Vamos a aplicarla para resolver estas actividades:



ACTIVIDAD 1. Calcula el área de estos círculos (fíjate que en unos te dan la medida del radio y en otros la medida del diámetro, no te confundas):

ACTIVIDAD 2.

ACTIVIDAD 3